Uncertainty is a multi-faceted characterization about data or predictions made from data that may include several concepts including error, accuracy, validity, quality, noise and confidence and reliability.
Uncertainty assessment tools are usually presented in a qualitative and a quantitative form, categorized into four levels (steps). The qualitative part summarizes all sources in a matrix, annotating direction, level of uncertainty and appraisal of the knowledge-base robustness. The quantitative tools possibly used include, sensitivity methods, error propagation techniques via Taylor expansion, Monte Carlo Modelling, Fuzzy methods and Bayesian modelling.
It is noted that the uncertainty present in these levels is accurately quantified and minimized based on elaborate statistical techniques. Therefore, the most important routes sources and pathways are delineated and further investigated.
Selected methods:
1) Sensitivity analysis methods are used to quantify the variation in model output that is caused by specific model inputs. Amongst others the optimal methods are the global sensitivity algorithms that take into account all the variation ranges of the inputs and apportion the output uncertainty to the uncertainty in the input factors (Figure 1).
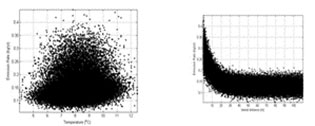
Figure 1. Global sensitivity scatter plots used to compute the contribution of input parameters to the estimated output (here pesticide emission).
2) A Monte Carlo simulation (MC) involves a large number of simulations from the distribution of the input parameters in the model that are combined to obtain values for the output parameters. For example, based on the distribution of the output, a risk level representing the high end (e.g., 95th percentile), central tendency (e.g., mean and median), or any other desired level of probability can be identified (Figure 2).
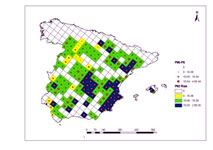
Figure 2. Health Risk and the associated uncertainty resulting from pesticide application on crops in Spain.
3) The most complex and exhaustive way of integrating uncertainty in a model is framed in a Bayesian perspective. The Bayesian philosophy considers that all uncertainty can be described by means of probability distributions, and is thus highly parametric. The basic concept of Bayesian philosophy is that of conditional distribution. The data (if available) are actively used and are assigned a probability distribution conditional on some parameters (e.g. data can be Gaussian conditional on the values of the mean and the variance). Moreover each parameter has a probability distribution (prior) that can include different degree of subjectivity the prior distribution will reflect higher probability to the values suggested by the expert or by the literature.
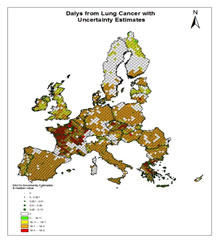
Figure 3. Computed DALYs and the associated computed uncertainty as a result of pesticide application in Europe.



